There have been quite a few overtime games in the NBA playoffs this year. We have had one in the finals already and in an earlier series between the Bulls and Celtics, 4 out of 7 games went into overtime, with one game in double overtime and one game in triple overtime!
How often should we expect a basketball game to end tied after 48 minutes of play? At first glance it would seem pretty rare. If you look at the distribution of points scored by the home teams and by the visiting teams separately, they look pretty close to a normal distribution with a large variance. If we made the crude hypothesis that the two distributions were statistically independent, then ties would indeed be very rare: 2.29% of all games would reach overtime.
But the scoring is not independent of course. Similar to a marathon, the amount of effort expended is different for the team currently in front versus the team trailing and this amount of effort also depends on the current point differential. But such strategy should have only a small effect on the probability of ties. The team ahead optimally slows down to conserve effort, balancing this against the increased chance that the score will tighten. Also, conservation of effort by itself should generally compress point differentials, raising not just the frequency of ties, but also the frequency of games decided by one or two points.
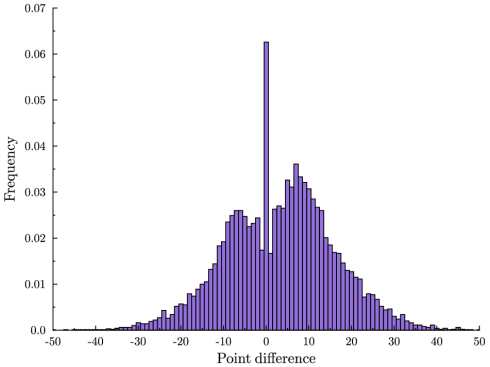
But overtime is almost 3 times more frequent than this: 6.26% of all NBA games are tied at the end of regulation play. And games decided by just a few points are surprisingly rare: It is more likely to have a tie than for the game to be decided by two points, and a tie is more than twice as likely as a one-point difference. These statistics are quite dramatic when you see them visually.
Here is a frequency histogram of the difference in points between the home team and visiting team at the end of regulation play. These are data from all NBA games 1997-2009. A positive number means that the home team won, a zero means that the game was tied and therefore went into overtime. Notice the massive spike at zero.
(There is also more mass on the positive end. This is the well-known home team bias.)
What explains this? A star PhD student at Northwestern, Toomas Hinnosaar, and I have been thinking about this. Our focus in on the dynamics and strategy at the end of the game. To give you some ideas, Toomas created the following striking video. It shows the evolution of the point differential in the last 40 seconds of the fourth quarter. At the beginning, the distribution looks close to normal. This is what the crude hypothesis above would predict. Watch how the spike emerges in such a short period of time.
By contrast, here is the same animation at the end of halftime. Nothing unusual.

37 comments
Comments feed for this article
June 11, 2009 at 12:55 am
Keith
I love reading posts like this. The spike at the end is crazy… I am interested in hearing your explanation.
Question: is there a similar sort of phenomenon in college basketball or even other sports where there is a relatively high amount of scoring?
June 11, 2009 at 7:11 am
Matt
Is the spike in overtime games a recent phenomenon? I think the NBA has rebounded in popularity since bottoming out after Jordan retired. Maybe there is a correlation.
June 11, 2009 at 12:37 pm
Chris
Interesting post. Doesn’t the 24 second clock drive this to an extent? E.g. if the score is tied already, the team with the ball has incentive to run down the clock for last shot. Defending team won’t foul to give free points.
However, the same could be said for a team down 1 or 2 points with possession of ball and <24 secs left…and there's not a similar spike. My hypothesis is that these teams face greater urgency to score, and will be more aggressive in taking an earlier, higher-percentage shot if it opens up, thus placing burden back on defense.
The difference between end of game and halftime is tougher to explain – bad coaching? Or less urgency by players?
June 11, 2009 at 1:02 pm
Donald A. Coffin
Interesting. I’m also looking forward to hypotheses about this.
Also…does the same phenomenon occur in NCAA games, or does the greater variation in team quality lead to a different outcome?
June 11, 2009 at 1:20 pm
James
The strategy changes in the last minutes of the game. It’s the only time in the game where teams intentionally foul.
June 11, 2009 at 1:27 pm
Frances
Maybe once it ties and only a few seconds are left, the team that controls the ball starts to waste time hoping that they can score at the very last second, which they often fail to. Does the same pattern appear at the end of the overtime?
June 11, 2009 at 1:41 pm
Jonathan Berman
My hypothesis is not that teams are actively looking for a strategy that will result in a tie, but rather that if they find themselves in a tie with less than 40 seconds remaining, they won’t behave in such a way that will danger losing that tie.
When the score is tied with less than 20 seconds or so, it seems that teams–and specifically, individual players on a team–begin to become risk averse (shooting less threes, trying not to foul, etc.)
What’s particularly interesting to me is the pattern that emerges just as the spike begins to develop. If you look closely at the first video, you see that the graph starts to spike around the 0 point differential, but creates a valley in the 4 to 7 points range differential. I imagine that is when losing teams *begin* to engage in risk seeking behavior (shooting low percentage shots, fouling, etc.) as they try to quickly claw their way back into the game.
It is of note that it is the risk adverse activities in basketball that lead to an odd number of points, namely fouling and shooting a three. These are the activities that “break” ties. It seems that the construct of the game of basketball is partially to blame. I wonder if we’d see a similar patter for games in which the scoring rules are more consistent (i.e. if there were no three pointers)?
June 11, 2009 at 1:50 pm
Christian
I would imagine it has to do with fouling and time rules. If a team had the option to take the ball out of bounds rather than shoot free throws, even just in the last two minutes of a game, I have to believe there would be far fewer overtime games.
In pro football at the end of each half, some offensive penalties result in a 10-second run-off. If something similar were adopted in basketball, no one would foul at the end of the game, the final few minutes would actually only take a few minutes, and the second half scoring differential would more closely resemble the first half.
June 11, 2009 at 1:55 pm
Anonimnik
Hm, how about them ratings? Everyone loves a tight game, including advertisers.
June 11, 2009 at 2:31 pm
cmac
Think the main factor is in pace change at the end of the game when the game is within 5 points. The winning team will slow its pace outside of its normal offense, which probably makes their offense less efficient (less points per possession).
On the other side, the losing team will increase its pace while the winning team starts playing soft defense (don’t want to foul in the last minute to give away free throws).
The combination makes the losing team more efficient and the winning team less efficient in the final minute, which should condense the # of outcomes towards zero.
June 11, 2009 at 4:43 pm
Mike H
This is really interesting, but it also seems pretty simple.
1. Teams down by 2 late are most likely to take a 2 point shot, while teams down by 3 will most often take a 3 point shot. The team’s choices make ties a likely outcome.
2. A Tie is a stable equilibrium, while other scores aren’t. If a team leads with the ball, they will be fouled, preventing the game from ending on that score. IF a team has the ball with a tie, they’ll usually be allowed to wait and take the last shot, either winning the game or leaving it as a tie.
June 12, 2009 at 1:33 am
Basket NBA, prolongations et anomalie statistique « Rationalité Limitée
[…] (les Lakers avaient déjà gagnés le match 2 après prolognation), on peut lire chez Cheaptalk ce billet de Jeff Ely ce billet au sujet du nombre anormalement élevé de matchs NBA qui vont en prolongation. […]
June 12, 2009 at 10:23 am
Vinnie
This is definitely good fodder for conspiracy theorists who are always looking for players and refs on the take or assume that one of David Stern’s henchmen is in the stands giving officials the “Keep it close, fellas” signal at the end of close games.
June 12, 2009 at 11:19 am
Applied Economics : Zoominac
[…] was found at Cheap Talk, with an explanation and videos. Warren found the link from The Sports Economist, where I found the […]
June 12, 2009 at 1:57 pm
Tyrone McCanna
In the late 90s or early 2000s, I forget when exactly, the NHL apparently felt this shift in endgame/overtime strategy, in which inferior teams were playing specifically for the tie, had become so much of a problem that they revamped the points system and guaranteed teams a point for making it to overtime, even if they eventually lost. I wonder what a graph like this would have looked like for the NHL right before they added the OT loss point? And I wonder if the OTL “fixed” the problem?
June 12, 2009 at 4:51 pm
Jim
What’s the old adage: you only have to watch the last two minutes of a NBA game. Perhaps it should be the last 40 seconds – plus overtime.
June 12, 2009 at 10:25 pm
More on Sorophilia in the NBA « Cheap Talk
[…] few of the commenters on the previous post nailed the late-game strategy behind the eye-popping animation. First, at the end of the game, the […]
June 14, 2009 at 5:25 pm
John
I believe this is mostly due to teams holding the ball for the last shot when the game is tied. The spike really begins to develop around the 24 second mark. Obviously if the game reaches a tie at any time inside the last 24 seconds the team with possession post tie is going to hold it for the last shot. As a result games that become tied at any time between 24 seconds and the end of the game are going to remain tied until the last second. This also explains the final frame where the frequency of a tie disappears (the team hit the last second shot).
June 15, 2009 at 4:46 pm
The overtime spike in NBA basketball | dv8-designs
[…] The distribution of point differentials at the end of NBA basketball games shows that a tie is more …. A possible simple explanation from the comments: 1. Teams down by 2 late are most likely to take a 2 point shot, while teams down by 3 will most often take a 3 point shot. The team’s choices make ties a likely outcome. […]
June 16, 2009 at 7:05 am
bobbygee
In the NBA the last two minutes are key. Reggie Miller scored ten points in less than ten seconds to give Inidana a huge win over the Knicks.. Bobby Gee check out my blog..http://bobbygee.wordpress.com/
June 16, 2009 at 10:56 am
DanF
It’s not just the use of fouls; timeouts are used to design plays with a higher chance to get a quick score. The team ahead will likely design a play during a timeout to take time off the clock before scoring. These plays have a lower chance of succeeding as the longer it takes the play to unfold, the more likely defense and random chance intervenes to bust the play.
June 16, 2009 at 11:00 am
Hugh
Its interesting that more games end in ties than might be expected, but your analysis seems flawed. You need to think in terms of situations that could produce overtime, it seems, and the one that you assume is ‘normal’ is that teams are trading equal baskets. But really, there are a lot of scenarios that could produce overtime. The dynamics of a game do change at the end of a game – teams that are behind and close start fouling like crazy. Sometimes this works and they can get it within a basket.
June 16, 2009 at 8:04 pm
Top Posts « WordPress.com
[…] The Overtime Spike in NBA Basketball There have been quite a few overtime games in the NBA playoffs this year. We have had one in the finals already and […] […]
June 29, 2009 at 1:41 pm
Watson F
It is not a strange thing! In every sports it is like this. Good article though.
July 17, 2009 at 8:22 am
Web shopping « Economic History Blog
[…] now for something completely different: Jeff Ely has a post on the strange tendency of basketball teams to go into overtime. I think, beyond a sport […]
August 13, 2009 at 11:13 pm
Arbitrage in Online Gambling « Cheap Talk
[…] can verify that arbitrage opportunites abound. In my research with Toomas Hinnosaar on sorophilia, we investigated an explanation involving betting. In the process we discovered that the many […]
July 2, 2010 at 8:53 pm
Nurkoonsdaz
The world was created by a single thought! scribd.com/doc/32556938
November 17, 2010 at 2:19 pm
Johan F
Interesting indeed.. I bet 5 on each game tonight. Odds approx 15x entry. 10 games.
January 26, 2011 at 12:41 pm
Richard Cooper
I wonder about the effect of the ability to stop the game multiple times in the last minute with timeouts and intentional fouls.
March 5, 2011 at 9:20 am
Cheep ticker | TheBeverages
[…] The Overtime Spike in NBA Basketball « Cheap TalkA blog about economics, politics and the random interests of forty-something professors … There have been quite a few overtime games in the NBA playoffs this year. We have had one in the finals already and in an earlier series between the Bulls and Celtics, 4 out of 7 games went into overtime, … What explains this? […]
December 24, 2011 at 5:18 pm
Nathan
I just read one of the comments about Michael Jordan retirement caused a basketball falling out for a while and i think maybe he’s right. For some reason though since the recession I’ve noticed a lot more enthusiam towards pro sports. Maybe it’s because its an escape from all the BS goin on around us, but for whatever the reason its happening..jump manual review
February 17, 2012 at 12:26 am
The points count the same no matter when they happen « The Unpersons
[…] it turns out there is more to a basketball game than the last 5 seconds. Games are often decided by more points, and those games are not quite as peachy for […]
December 7, 2012 at 1:38 pm
Watchmaker
The quality of this data is amazing. What’s your source? I have a not-strictly-academic interest in this topic.
December 7, 2012 at 1:41 pm
jeff
publicly available, just scraped from (as i recall) nba.com
February 7, 2013 at 12:28 am
Watchmaker
Thanks. More proof that I need to graduate from R to Python.
June 8, 2015 at 3:56 pm
Statisticator
Redid a similar analysis looking at more recent data (2009-2015), same phenomenon emerges! I also looked at regular season vs playoffs and if the same effect occurs at the end of overtimes:
http://statisticator.blogspot.com/2015/06/the-overtime-effect-why-things-go-crazy.html
January 7, 2016 at 1:21 pm
adult video
The Wireless HD Media Player has a High Definition Multimedia Interface that.
If you pay video games for a long period of time,
you can wear out your eyes and your hands.
It’s not good to sit doing the same thing for long periods
of time.